CBSE class 12 maths integration chapter in the new syllabus will come in 2nd term. Here is all the information you need. Important questions, previously asked questions, solutions.
Integration chapter 7 of NCERT Maths book class 12 is one of the important exercises from exam point of view. The new revised syllabus 2022 is divided into two terms. Calculus alone carries 18 marks out of 50. therefore integration is a very important chapter this year. Here are some of the very important previously asked questions of integration.
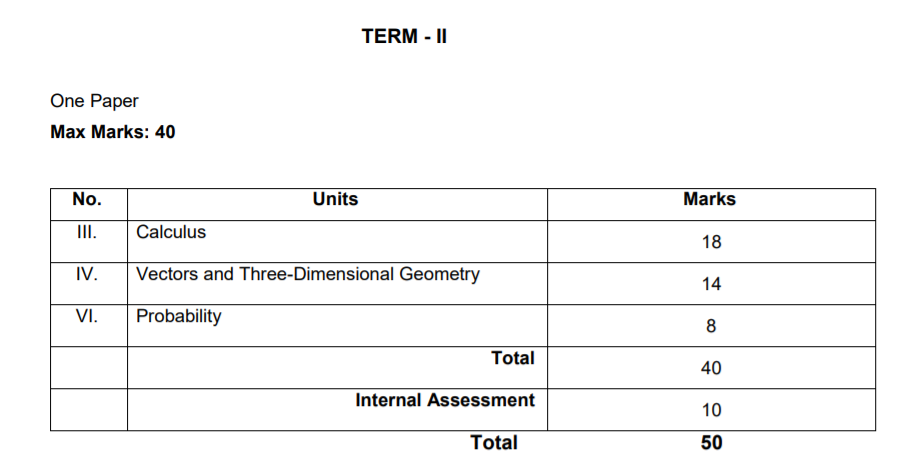
Chapters under calculus are (2nd term exam new syllabus)
1. Integrals
2. Application of integrals
3. Differential equations
All these questions are previously asked questions. [Download pdf]
- \int \frac{3-5sin x}{\cos^2 x} dx [2018]
- \int \frac{4}{(x-2)(x^2+4)} dx [2018]
- \int_{0}^\frac{\pi}{2} \frac{x \sin x \cos x}{\sin^4 x + \cos^4 x} dx [2018]
- \int_{1}^3 (3x^2+2x+1) dx as the limit of sum. [2018]
- \int \frac{dx}{\sqrt{2x-x^2}} [2019]
- \int \frac{dx}{\cos^2 x(1-\tan x)^2} [2019]
- \int_{0}^1 x(1-x)^n dx [2019] [2020]
- \int \frac{\cos x}{(1+\sin x)(2+\sin x)} dx [2019]
- \int_{0}^\pi \frac{x\sin x}{1+\cos^2x} dx [2019]
- \int \frac {e^{2x}-1}{e^{2x}+1} dx Solution
All the Question below are asked in CBSE Maths class 12 exam 2020 - \int_{\frac{-\pi}{4}}^\frac{-\pi}{4} \sec^2x dx
- \int x^4\ln x dx
- \int \frac{2x}{\sqrt[3]{x^2+1}} dx
- \int_{1}^3 |2x-1| dx
- \int \frac{dx}{9-4x^2}
- \int \sec^3x dx
- \int_{\frac{-\pi}{2}}^\frac{\pi}{2} x \cos^2x dx
- \int \frac{\tan^3x}{\cos^3x} dx
- \int \frac{x^3+1}{x^3-x} dx
- \int e^x(\frac{x\ln x +1}{x}) dx
- \int_{-2}^2 |x| dx
- \int\frac{dx}{9+4x^2}
- \int_{-1}^2 |x^3-x| dx
- \int_{0}^\frac{\pi}{8} \tan^2(2x) dx
- \int_{0}^{2\pi} |\sin x| dx
- \int_{0}^a \frac{dx}{1+4x^2} = \frac{\pi}{8} find the value of a.
- \int \frac{dx}{\sqrt {x} +x}
- \int \sin^5 \frac{x}{2} \cos \frac{x}{2} dx
- \int x^2 e^{x^3} dx
- \int_{1}^4 |x-5| dx
- \int \frac{x}{x^2+3x+2} dx
- \int_{1}^2 [\frac{1}{x} - \frac{1}{2x^2}]e^{2x} dx
- \int_{1}^4 (x^2-x) dx as a limit of sum
Solutions to these questions will be available soon on our youtube channel and the notes will be posted here. stay tuned
Recommended videos:
Also read:
Evaluate the Integral: ∫ (tan(x/2)+cos(x/2)) / sin(x/2) dx