Q. The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?

Ans:
let the equal sides of the isosceles triangle be “x”,
the base of the triangle is fixed and is “b” (constant).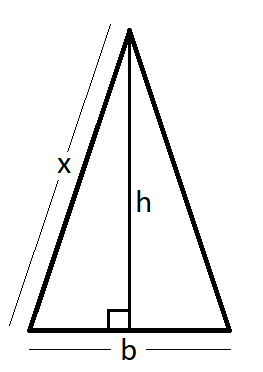
height of the triangle = \sqrt (x^2-\frac{b}{4}^2)
a/q \frac{dx}{dt}= 3 m/s
also, Area of triangle is = 1/2 x base x height
i.e. A=\frac{1}{2}*b*\sqrt(x^2-\frac{b}{4}^2)
or A=\frac{b}{4}\sqrt(4x^2-b^2)
\frac{dA}{dt}=\frac{b}{4}\frac{8x}{2\sqrt(4x^2-b^2)}\frac{dx}{dt}
Now, when equal sides are equal to the base i.e. x=b
\frac{dA}{dt} at x= b
\frac{dA}{dt}= \frac{8b^2}{8\sqrt(4b^2-b^2)}3
or \frac{dA}{dt}= \frac{8b^2}{8\sqrt(3b^2)}3
or \frac{dA}{dt}= \frac{3b}{\sqrt3}
or \frac{dA}{dt}= \sqrt3b
Thus, Area is decreasing at the rate of \sqrt3b cm^2/s