- A derivative is a mathematical tool used to find the ratio between two quantities like – Distance and Time, Force and Area, in general, it is a ratio between y and x (where y and x are two quantities not necessarily different).
- This tool helps to find ratios even if the change is infinitesimally small.
- To find the derivative one need to have a relationship between the two quantities (i.e., a function).
- The ratio can be expressed as follows:
lim_{h→0}\frac {f(x+h) −f(x) }{h}
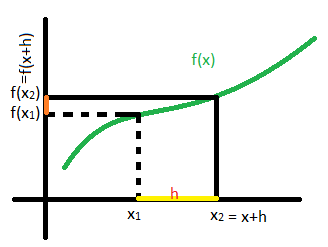
Where h is a infinitesimal change in “x” and f(x+h)-f(x) is the change in “y”
lim_{h→0}\frac {f(x+h) −f(x) }{h} is denoted by the symbol \frac{dy}{dx}
- The change in x is so small that the two points (initial and final points of x) overlap and can be considered as a single point so the derivative here is usually called derivative at a point. As the change in x is infinitesimally small, we say the gap between them tends to zero I.e. h→0
Example
Find the derivative of y=x^2 at x=10
\frac{dy}{dx} = lim_{h→0}\frac {f(x+h) −f(x) }{h}
\frac{dy}{dx} = lim_{h→0}\frac {(x+h)^2 −x^2 }{h}
\frac{dy}{dx} = lim_{h→0}\frac {x^2 +2xh +h^2 −x^2 }{h}
\frac{dy}{dx} = lim_{h→0}\frac {2xh +h^2 }{h}
\frac{dy}{dx} = lim_{h→0}\frac {h(2x +h)}{h}
\frac{dy}{dx} = lim_{h→0}(2x +h)
\frac{dy}{dx} =2x
thus, derivative at x=10 is \frac{dy}{dx}|_{x=10} =2(10) = 20
Remark: \frac{dy}{dx} =2x is a general derivative for all x belongs to domain.
Many times the dervaties are not easy to determine due to complexity of limit. So to determine the derivative one need to have a good grip on limit calculation.
For practical usage, the derivatives of some simple functions are directly used to find derivatives of complex ones. To do so algebra of derivatives is required. we are now going to study the algebra of derivatives next.
Algebra of derivatives:
Note: \frac{df}{dx} can also be represented as f'(x)
Let f(x) and g(x) be two functions defined on the same domain
- \frac{d(f+g)}{dx} = \frac{df}{dx} + \frac{df}{dx}
- \frac{d(f-g)}{dx} = \frac{df}{dx} - \frac{df}{dx}
- Product rule / Leibnitz rule
\frac{d(f.g)}{dx} = \frac{df}{dx} g(x)+ f(x)\frac{dg}{dx} - Quotient Rule
\frac{d(\frac{f}{g})}{dx} = \frac{ \frac{df}{dx} g(x)- f(x)\frac{dg}{dx}}{{g(x)}^2} , where g(x)\neq 0
Example
find a derivative of y= x^2sinx
before we start we should note that the general derivatives of functions f(x)= x^2 and g(x)=sinx is 2x and cosx respectively and x^2sinx is a product of them.
so, \frac{d(f.g)}{dx} = \frac{df}{dx} g(x)+ f(x)\frac{dg}{dx}
\frac{d(x^2sin x )}{dx} = \frac{d(x^2)}{dx} sin x+ x^2\frac{d(sin x)}{dx}
\frac{d(x^2sin x )}{dx} = 2x sin x+ x^2cos x
Also Read: CBSE class 12 maths integration important questions 2022