Q. Show that the normal at any point \Theta to the curve
x= acos\theta + a \theta sin\theta , y = a sin\theta-a\theta cos\theta
is at a constant distance from the origin.

Ans:
Note:- This question needs prior knowledge of
The perpendicular distance from a point to the line
i.e.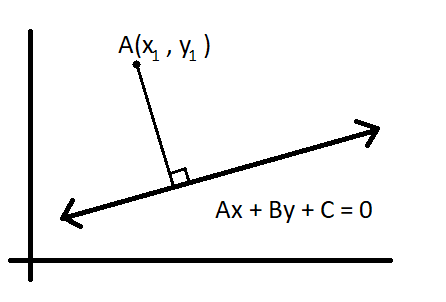


\therefore AL = \frac{|Ax_1 + By_1 + C|}{\sqrt(A^2 + B^2)}
Now,
x= acos\theta + a \theta sin\theta
\frac{dx}{d\theta} = -a sin\theta + a(sin\theta + \theta cos\theta)
or \frac{dx}{d\theta} = a\theta cos\theta
Also,
y = a sin\theta-a\theta cos\theta
\frac{dy}{d\theta} = a cos\theta - a(cos\theta + (-sin\theta) \theta)
\frac{dy}{d\theta} = a \theta sin\theta
thus,
\frac{dy}{dx} = \frac{a\theta sin\theta}{a \theta cos\theta}
or \frac{dy}{dx} = tan\theta

\therefore slope of normal be = \frac{-1}{tan\theta}
Now,
Equation of normal at (acos\theta + a \theta sin\theta, a sin\theta-a\theta cos\theta)
y - a sin\theta+a\theta cos\theta = \frac{-1}{tan\theta}( x - acos\theta - a \theta sin\theta)
or y tan\theta - a sin\theta tan\theta +a\theta cos\theta tan\theta = -x + acos\theta + a \theta sin\theta)
or y tan\theta - a sin\theta tan\theta +a\theta sin\theta = -x + acos\theta + a \theta sin\theta
or y tan\theta + x = \frac{a sin^2\theta}{cos\theta} + a cos\theta
or y tan\theta + x = \frac{a sin^2\theta +a cos^2\theta}{cos\theta}
or y tan\theta cos\theta + x cos\theta = a
or y sin\theta + x cos\theta - a =0
thus,
Distance of curve from origin is,
= \frac{|sin\theta .0 + cos\theta .0 - a|}{\sqrt(sin^2\theta + cos^2\theta)}
= |-a|
= a
here distance is independent of \theta and equal to a which is a constant.