Q.Find the intervals in which the function f given by
f(x)=\frac{4sinx-2x-xcosx}{2+cosx}
is (i) increasing (ii) decreasing.

Ans:
f(x)=\frac{4sinx-2x-xcosx}{2+cosx}
f'(x)=\frac{4cosx-2-(cosx-xsinx)(2+cosx)-(-sinx)(4sinx-2x-xcosx)}{(2+cosx)^2}
or f'(x)=\frac{4cosx-2-cosx+xsinx)(2+cosx)+sinx(4sinx-2x-xcosx)}{(2+cosx)^2}
or f'(x)=\frac{3cosx+xsinx-2)(2+cosx)+sinx(4sinx-2x-xcosx)}{(2+cosx)^2}
or f'(x)=\frac{6cosx+2xsinx-4+3cos^2x+xsinxcosx-2cosx+4sin^2x-2xsinx-xcosxsinx}{(2+cosx)^2}
or f'(x)=\frac{4cosx-4+3cos^2x+4sin^2x}{(2+cosx)^2}
or f'(x)=\frac{4cosx-4(1-sin^2x)+3cos^2x}{(2+cosx)^2}
or f'(x)=\frac{4cosx-4cos^2x+3cos^2x}{(2+cosx)^2}
or f'(x)=\frac{4cosx-cos^2x}{(2+cosx)^2}
Now
f'(x)=0
\implies 4cosx-cos^2x = 0
or cosx(4-cosx)=0
\therefore cosx=0, cosx=4
cosx= 4 is not possible as -1<cosx<1
cosx= 0 \implies x=\frac{\pi}{2},\frac{3\pi}{2}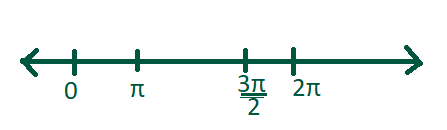

f'(x)=\frac{cosx(4-cosx)}{(2+cosx)^2}
\implies f'(x)>0 for x \epsilon (0,\frac{\pi}{2}) and x \epsilon (\frac{3\pi}{2},2\pi)
As, 0<cosx<1 for x \epsilon (0,\frac{\pi}{2}) and x \epsilon (\frac{3\pi}{2},2\pi)
\therefore f is increasing in (0,\frac{\pi}{2}) (\frac{3\pi}{2},2\pi)

f'(x)<0 for x \epsilon (\frac{\pi}{2},\frac{3\pi}{2})
As, -1<cosx<0 for x \epsilon (\frac{\pi}{2},\frac{3\pi}{2})
\therefore f is decreasing in (\frac{\pi}{2},\frac{3\pi}{2})